I’m a stock market enthusiast 📈, so lately I have spent my spare time on the topic of stock option pricing, and I was curious to find out whether or not I could build a script that accurately reflected real market option prices. It turns out I came close, and learned a lot along the way, which I share in this article.

My analysis uses the Monte Carlo method for pricing options, which from all available pricing models in the literature is the most straight forward, practical one for a software developer to start working with, when compared to closed form, analytic models, such as the Black–Scholes model.

The code I share in this article is written in the R programming language, using the following packages: sfsmisc, plotly, ggplot2.

Data Set

I had to pick a stock to work on as the starting point, so I decided to use PETR4 which is the most actively traded stock in B3, the largest stock exchange in Brazil, and also the stock with the most actively traded options.

On December 17, 2019, while PETR4 was priced at R$ 29.71, I spoted the following european call option prices:

The maturity of these options is the same, January 20, 2020, i.e., 20 business days from the recorded prices date. I saved this data into a CSV formatted file that you can find here.

Besides that I also used six months worth of daily PETR4 log returns from 17/Jun/2019 to 16/Dec/2019 (126 samples), which you can find here.

Distribution of Stock Returns

Under the Monte Carlo method, in order to calculate the price of a stock option, first we need a probability distribution model of the stock returns. Let’s take a look at the probability density estimate for our stock:

x <- read.table("PETR4_Returns.txt")[["V1"]]

d_real <- density(x)
df <- data.frame(x = d_real[["x"]], y = d_real[["y"]])

p <- ggplot() +
  ggtitle("PETR4 daily returns density estimate") +
  geom_line(data = df, aes(x=x, y=y), colour="black") 
ggplotly(p)

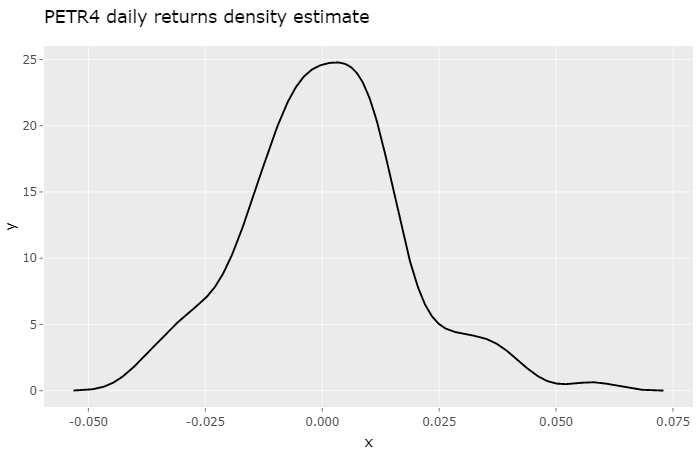
Because the number of samples is small, we don’t get that fine-looking symmetric density estimate we would like. Instead, what we get is a density estimate somewhat sensitive to trends and macroeconomical events of this six month period. If we were to look at the previous six month period this observed density estimate would certainly show differences.

The next step is to find a model that reasonably fits this observed density. While there isn’t an agreement on which probability density function best describes stock returns, I decided to turn to two notable, widely adopted, basic functions, the Gaussian distribution and the Cauchy Distribution.

Guassian Model

Let’s try to fit a Gaussian density function to our market data, and see what it looks like. First I will define a couple of auxiliary functions:

# generates a truncated gaussian density
dgauss <- function(std, mean, min, max) {
  d.x <- (0:511) * (max - min) / 511 + min
  d.y <- dnorm(d.x, mean, sd = std)
  d.y <- d.y / integrate.xy(d.x, d.y)
  f <- data.frame(x = d.x, y = d.y)
  return (f)
}

# interpolates data frame
interpolate <- function(df, min, max, n) {
  step <- (max - min) / n
  pol <- data.frame(
    with(df, 
         approx(x, y, xout = seq(min, max, by = step))
    )
  )
  return (pol)
}

# simple numeric maximum likelihood estimation
# (resolution reffers to that of daily log returns)
mle <- function(dist, x) {
  min_x <- min(x)
  max_x <- max(x)
  resolution <- 10000
  n = (max_x - min_x) * resolution
  rev <- interpolate(data.frame(x = dist$x, y = dist$y), min_x, max_x, n)
  indexes = sapply(x, function (x) { return ((x - min_x) * resolution + 1) })
  return (log(prod(rev$y[indexes])))
}

With these functions I developed a simple brute force script to find the Gaussian distribution standard deviation that best fits the observed density estimate:

max_mle <- -Inf
d_norm <- c()

for(k in seq(0.001, 0.1, by = 0.0001)) {
  dist <- dgauss(k, mean(x), -6 * sd(x), 6 * sd(x))
  val <- mle(dist, x)
  if (val > max_mle) {
    d_norm <- dist
    max_mle <- val
  }
}

df1 <- data.frame(x = d_real[["x"]], y = d_real[["y"]])
df2 <- data.frame(x = d_norm[["x"]], y = d_norm[["y"]])

p <- ggplot() +
  ggtitle("Probability densities") +
  scale_colour_manual("", values = c("red", "blue")) +
  geom_line(data = df1, aes(x=x, y=y, colour="Observed")) +
  geom_line(data = df2, aes(x=x, y=y, colour="Gaussian"))
ggplotly(p)

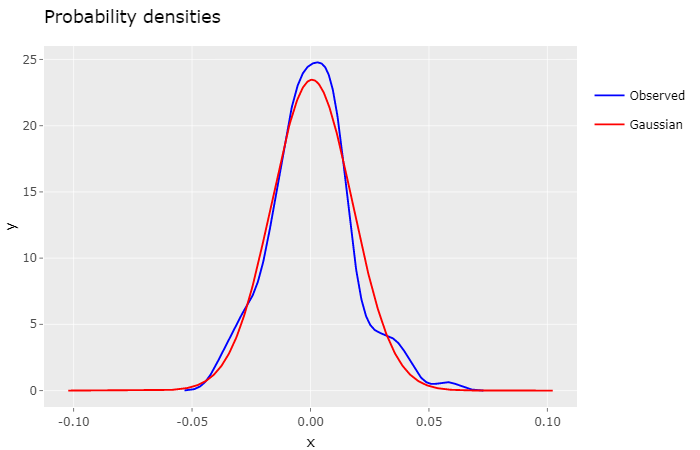
Both densities display a similar shape, but it’s perceptible that the Gaussian density decreases marginally faster than the observed density.

Despite the fact that the Gaussian distribution is widely used in fianacial models, it has some well known pitfalls, namely its inability to encompass fat tails observed in historical market data. As a result it will fail accurately describe extreme volatility events, which can lead to possibly underpriced options.

Cauchy Model

The Cauchy distribution, just like the Gaussian distribution, is a stable distribution, but one with fat tails. Over the years several academic papers have looked into it as an alternative to best describe these extreme volatility events.

So let’s see how it performs. Initially, I defined the following auxiliary function in order to fit it to the observed density.

# generates a truncated cauchy density
dcauchy <- function(s, t, min, max) {
  d.x <- (0:511) * (max - min) / 511 + min
  d.y <- 1 / (s * pi * (1 + ((d.x - t) / s) ^ 2))
  d.y <- d.y / integrate.xy(d.x, d.y)
  f <- data.frame(x = d.x, y = d.y)
  return (f)
}

The brute force fitting script is the same as the previous one, replacing the call to dgauss with dcauchy:

max_mle <- -Inf
d_cauchy <- c()

for(k in seq(0.001, 0.1, by = 0.0001)) {
  dist <- dcauchy(k * (sqrt(2/pi)), mean(x), -6*sd(x), 6*sd(x))
  val <- mle(dist, x)
  if (val > max_mle) {
    d_cauchy <- dist
    max_mle <- val
  }
}

df1 <- data.frame(x = d_real[["x"]], y = d_real[["y"]])
df2 <- data.frame(x = d_cauchy[["x"]], y = d_cauchy[["y"]])

p <- ggplot() +
  ggtitle("Probability densities") +
  scale_colour_manual("", values = c("red", "blue")) +
  geom_line(data = df1, aes(x=x, y=y, colour="Observed")) +
  geom_line(data = df2, aes(x=x, y=y, colour="Cauchy"))
ggplotly(p)

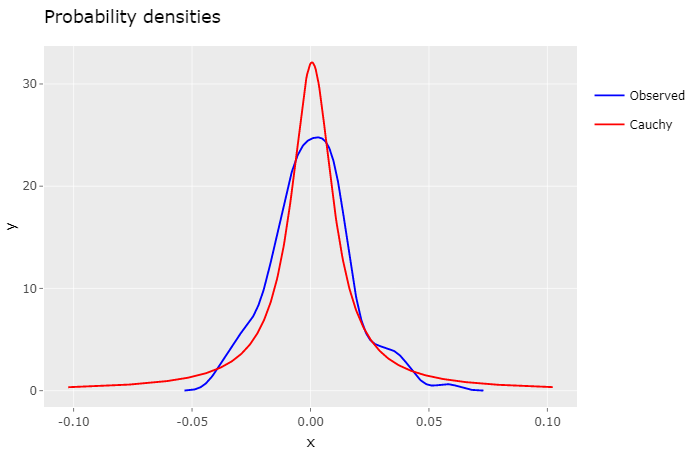
Intuitively, by looking at this plot, it feels that the Cauchy density isn’t as much as a good fit as the Gaussian density. Indeed, the log-likelihood ratio of the Gaussian Model to the Cauchy Model is 7.5107, quite significant.

The general consensus for the Cauchy distribution is that it has too fat tails, which in our case may lead to overpriced options. Nevertheless, it can be very useful for defining a high volatility scenario for risk analysis.

Now that we have our probability distribution models we can go ahead and calculate option prices based on them.

Option Pricing

The technique applied to calculate the fair price of an option under the Monte Carlo method is:

(1) to generate a large number of possible, but random, price paths for the underlying stock via simulation, and (2) to then calculate the associated exercise value (i.e. “payoff”) of the option for each path. (3) These payoffs are then averaged and (4) discounted to today. This result is the value of the option.¹

To accomplish that I defined, yet again, more auxiliary functions:

# generates random samples for a probability density
dist_samples <- function(dist, n) {
  samples <- (approx(
    cumsum(dist$y)/sum(dist$y),
    dist$x,
    runif(n)
  )$y)
  samples[is.na(samples)] <- dist$x[1]
  return (samples)
}

# calculates the expected value of a probability density
exp_val <- function(dist) {
  v <- dist[["x"]] * dist[["y"]]
  return (sum(v) / sum(dist[["y"]]))
}

# converts a single day probability density to a n-day period
# (removes any drift from the input density)
dist_convert <- function(dist, n) {
  dd <- data.frame(x = dist$x - exp_val(dist), y = dist$y)
  dn <- density(sapply(1:100000, function(x) (sum(dist_samples(dd, n)))))
  return (dn)
}

# calculates the price of a call option from a probability density
call_price <- function(dist, strike, quote) {
  v <- (((exp(1) ^ dist[["x"]]) * quote) - strike) * dist[["y"]]
  v <- pmax(v, 0)
  return (sum(v) / sum(dist[["y"]]))
}

And here’s the final script for calculating option prices based on the fitted Gaussian and Cauchy distribution, for each strike price, and then plot the result against actual (Bid) prices:

stock_quote <- 29.71
days_to_maturity <- 20

df1 <- read.csv("PETR4_Calls.txt", header = TRUE, sep = ";")
strikes <- df1[["Strike"]]

dn <- dist_convert(d_norm, days_to_maturity)
y2 <- sapply(strikes, function(x) call_price(dn, x, stock_quote))
df2 <- data.frame(x = strikes, y = y2)

dn <- dist_convert(d_cauchy, days_to_maturity)
y3 <- sapply(strikes, function(x) call_price(dn, x, stock_quote))
df3 <- data.frame(x = strikes, y = y3)

p <- ggplot() +
  ggtitle("Option Prices") +
  xlab("Strike Price") +
  ylab("Option Price") +
  scale_colour_manual("", values = c( "black", "red", "blue")) +
  geom_line(data = df1, aes(x=Strike, y=Bid, colour="Actual")) +
  geom_line(data = df2, aes(x=x, y=y, colour="Gaussian")) +
  geom_line(data = df3, aes(x=x, y=y, colour="Cauchy"))
ggplotly(p)

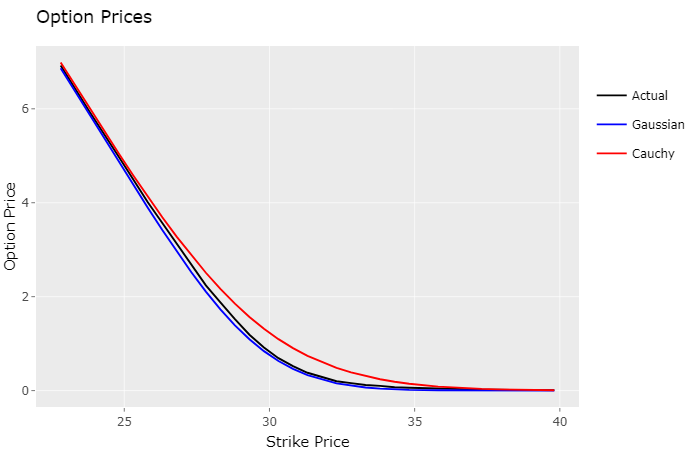
As speculated, actual market prices are slightly above the Gaussian model prices (underpriced), and below the Cauchy model prices (overpriced). The Gaussian model came really close to the actual option prices, which makes sense, since it’s likelihhod to the observed density was much higher.

So after analysing this plot I had an idea, since this final script can take any probability density to calculate option prices, what if I used the observed density estimate instead, would it yield better, more accurate option prices?

stock_quote <- 29.71
days_to_maturity <- 20

df1 <- read.csv("PETR4_Calls.txt", header = TRUE, sep = ";")
strikes <- df1[["Strike"]]

dn <- dist_convert(d_real, days_to_maturity)
y2 <- sapply(strikes, function(x) call_price(dn, x, stock_quote))
df2 <- data.frame(x = strikes, y = y2)

p <- ggplot() +
  ggtitle("Option Prices") +
  xlab("Strike Price") +
  ylab("Option Price") +
  scale_colour_manual("", values = c( "black", "red")) +
  geom_line(data = df1, aes(x=Strike, y=Bid, colour="Actual")) +
  geom_line(data = df2, aes(x=x, y=y, colour="Empirical"))
ggplotly(p)

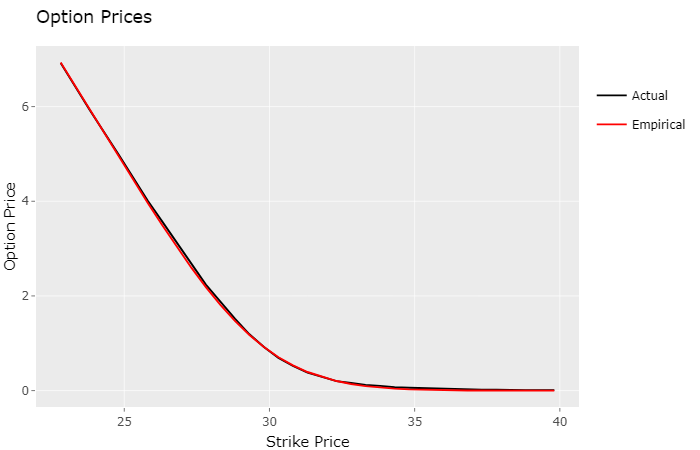
In fact, to my surprise, it did. Visually the lines appear to be on top of each other. The table below displays the standard deviation from the models estimates to the actual market prices:

Conclusion

The “empirical” model turned out to be the one that best approximates market prices, for this particular stock (PETR4) in the B3 stock exchange. Market option prices are determined by automated trading systems, usually employing much more sophisticated techniques than the one presented here, in real-time, almost instantaneously reflecting price shifts of the underlying stock. Even so, this simplified approach yielded great results, worth exploring more deeply.

Notes

• I submitted this article on Hacker News and it received a lot of attention there. One comment correctly pointed out that the standard technique for fitting probability distributions is to use maximum likelihood estimation (MLE), instead of the least squares regression approach that I originally employed. So I ran the analysis again using MLE, observed improved results for both models, and updated the code and plots.
• I also fixed a minor issue in the function that generates random samples for probability densities, and recalculated the “empirical” model standard deviation.
• For reference you can find the original article here.

Sources

[1] Don Chance: Teaching Note 96-03: Monte Carlo Simulation

Recent claims from Google of achieving “Quantum Supremacy” brought a lot of attention to the subject of Quantum Computing. As a software developer all of the sudden every non-developer person I know started asking me questions about it, what it meant, and if it’s the start of skynet 🤖

I knew only the basic stuff from college, general concepts from quantum mechanics and superposition, but barely grasped how it was actually applied to computing and algorithms. So I decided to study it more deeply and develop a weekend project along the way.

I’m sharing my learnings in this post focusing on the programmer’s perspective of quantum computing, and demystifying the almost supernatural facet the general media gives to it. It’s basically just linear algebra.

My weekend project turned out to be a pet Quantum Simulator, which I made available on github.

The Qubit

Qubit is the basic unit of quantum information. You can think of it as a variable that when measured gives you either true or false, i.e., a boolean value. For instance:

var q = new Qubit(true);

Assert.IsTrue(q.Measure());

As a variable, you can perform operations on qubits, such as applying the “X gate” to negate its value:

var q = new Qubit(true);

new XGate().Apply(q);

Assert.IsFalse(q.Measure());

Now things get more interesting, the quibit’s value, or state, can also be in a coherent superposition, being both true and false at the same time, with 50% ~ 50% probability (adding up to 100%). To achieve that we apply an “H gate” (Hadamard gate) to it:

var q = new Qubit(false);

new HGate().Apply(q);

// will print 'true' half of the time, 'false' the other half
Console.Write(q.Measure());

To understand what this means we need to take a look at the Qubit’s internal state. It’s actually an array of complex numbers. Considering a single qubit system we can have:

• [1, 0] → 100% chance of being measured 0 (false)
• [0, 1] → 100% chance of being measured 1 (true)
• [1 / sqrt(2), 1 / sqrt(2)] → 50% chance of being measured 0 and 50% chance of being measured 1

OBS: The correct mathematical notation of a quantum state of “n” qubits is a vector of a single column and 2ⁿ rows. Here I’m describing how to implement it in code, using arrays.

The first position of the array holds a complex number describing the probability of the qubit being “0”, and the second position of it being “1”. The probability for each outcome is calculated as the complex number magnitude squared.

Each quantum gate is a matrix that operates on the quantum system state. For example, I implemented the “H Gate” as a UnaryOperation in my project:

public class HGate : UnaryOperation
{
    protected override Complex[,] GetMatrix()
    {
        return h_matrix;
    }

    private readonly Complex[,] h_matrix = new Complex[,]
    {
        { 1 / Math.Sqrt(2), 1 / Math.Sqrt(2) },
        { 1 / Math.Sqrt(2), -1 / Math.Sqrt(2) }
    };
}

So the “H gate” took the qubit from the [1, 0] state to the [1 / sqrt(2), 1 / sqrt(2)] state through a matrix multiplication, implemented as follows:

public static Complex[] Multiply(Complex[,] matrix, Complex[] vector)
{
    if (matrix.GetLength(0) != vector.Length)
        throw new InvalidOperationException();

    var r = new Complex[vector.Length];

    for (int i = 0; i < matrix.GetLength(0); i++)
    {
        r[i] = 0;
        for (int j = 0; j < matrix.GetLength(1); j++)
            r[i] += vector[j] * matrix[i, j];
    }

    return r;
}

You can define different 2x2 matrices to operate on a single qubit, but there’s a catch, quantum gates must be reversible (due to physical world constraints), i.e., applying it twice should reverse its effects:

var q = new Qubit(false);

new HGate().Apply(q);
new HGate().Apply(q);

Assert.IsFalse(q.Measure());

This reversibility is also required for more complex quantum gates, operating on multiple qubits as we’ll see in the next section.

Quantum Entanglement

The potential of quantum computing becomes more apparent when we start using gates that operate on two or more qubits. Perhaps the most famous binary quantum gate is the “CNOT gate” (CXGate class in my project), which will negate the target qubit if a control qubit is true, otherwise it preserves the target qubit:

var control = new Qubit(true);
var target = new Qubit(false);

new CXGate().Apply(control, target);

Assert.IsTrue(target.Measure());

The “CNOT gate” defines a 4x4 matrix that is applied to the two qubit system state. Here’s how I implemented it:

public class CXGate : BinaryOperation
{
    protected override Complex[,] GetMatrix()
    {
        return cx_matrix;
    }

    private readonly Complex[,] cx_matrix = new Complex[,]
    {
        { 1, 0, 0, 0 },
        { 0, 1, 0, 0 },
        { 0, 0, 0, 1 },
        { 0, 0, 1, 0 }
    };
}

As expected the two qubit quantum system state vector will have length “4” (Length = 2ⁿ), representing four exclusive values, and superpositions of them:

• [1, 0, 0, 0] → 100% chance of being measured 0
• [0, 1, 0, 0] → 100% chance of being measured 1
• [0, 0, 1, 0] → 100% chance of being measured 2
• [0, 0, 0, 1] → 100% chance of being measured 3

To derive the four position state vector from the two qubits, simply perform their tensor product, for instance:

• [1, 0] ⦻ [0, 1] = [0, 1, 0, 0]

Which is equivalent to |0⟩ ⦻ |1⟩ = |01⟩ using Dirac notation.

Now supose that, before applying the “CXGate”, we apply the “HGate” to the control bit, what would happen?

var control = new Qubit(true);
var target = new Qubit(false);

new HGate().Apply(control);
new CXGate().Apply(control, target);

// What to expect for:
// control.Measure() ?
// target.Measure() ?

We’ve seen before that the control qubit will be in a coherent superposition state, then it will be applied to the “CXGate”, modifying the target qubit. From a classical point of view there are two valid scenarios:

• Control qubit is 0 and target qubit is preserved as 0
• Control qubit is 1 and target qubit is flipped to 1

Which one will be? Actually both of them!

If you measure one qubit (control or target - you choose), you have 50% of chance for each outcome, either 0 or 1. But after that the quantum state collapses, and we will have 100% certainty of the next measurement outcome, since there are only two valid states for this system. The value of one qubit dictates the value of the other. The qubits are entangled.

Algebraically this entangled state is describe as:

• [1/sqrt(2), 0, 0, 1/sqrt(2)] → 50% chance of being measured 0 (|00⟩) and 50% chance of being measured 3 (|11⟩)

There is no possible outcome where values 1 (|01⟩) or 2 (|10⟩) are measured.

Quantum Collapse

Measuring, or “collapsing”, a single quibit is easy, as explained above it has only two possible outcomes, each one with a defined probability. It behaves as a random variable.

As more qubits are added to the quantum system and become entangled, measuring one quibit can have a direct impact on other quibits, collapsing their probability distribution. A practical implementation for measuring a single qubit in a multiple qubit system, extracted from my Qstate class, follows:

int val = Sample();
bool m = BinaryUtility.HasBit(val, pos);
Collapse(pos, m);

Initially it samples the quantum system state vector in full, without changing it, getting an outcome for the 2ⁿ system. If we wanted to measure all system qubits at once, we could simply collapse the entire state vector from this sample, however we are only interested in measuring one qubit, leaving others unmeasured.

So after getting a full sample we test for the bit being measured. It could be present in the sample, in which case it will collapse to true, or not present, collapsing to false. Once we get its value we propagate it to the state vector:

private void Collapse(int pos, bool b)
{
    for (int i = 0; i < v.Length; i++)
        if (BinaryUtility.HasBit(i, pos) != b)
            v[i] = Complex.Zero;

    var sum = Math.Sqrt(
        v.Sum(x => x.Magnitude * x.Magnitude)
    );
    for (int i = 0; i < v.Length; i++)
        v[i] /= sum;
}

This method will zero out all positions in the state vector in which this quibit has a different value than what was measured. Then it will normalize the vector, making sure the sum of the complex numbers magnitudes squared adds to one.

From a logical point of view this is what “quantum collapse” means, we measured one qubit and propagated its value to the quantum state vector, “zeroing” the probability of all outcomes inconsistent with this measurement.

Beating Classical Computing

Saving the best for last, I will now introduce the Deutsch Oracle algorithm, one of the first examples of a quantum algorithm that is exponentially faster than its classical counterpart on the size of the input.

Its quantum circuit diagram is presented below:

figure 1. Deutsch algorithm circuit diagram

The purpose of this algorithm is to determine if an unknown function f(x) is either balanced or constant. Considering the one quibit case (n = 1) there are two balanced functions, the identity and the negation functions:

And two constant functions, the “set to zero” and the “set to one” functions:

The algorithm circuit will become more clear after we translate it to code, considering an unknown one qubit input function f(x) implemented by a binary quantum gate:

public class DeutschAlgorithm
{
    public bool IsBalanced(BinaryOperation gate)
    {
        var q1 = new Qubit(false);
        var q2 = new Qubit(true);

        new HGate().Apply(q1);
        new HGate().Apply(q2);

        gate.Apply(q2, q1);

        new HGate().Apply(q1);

        return q1.Measure();
    }
}

Classically we would require two measurements to find out the answer. For instance, if we query the {0 → 0} input/output pair, we are not sure yet if this is an identity or “set to zero” function.

In quantum computing however, we can find out the answer with a single query! I will not get into the details of the circuit inner workings, only say that it takes advantage of superposition to reduce the number of queries required to get a conclusive answer.

To see the math behind it open the link provided at the start of this section. You can also debug the algorithm executing one of my project unit test classes: DeutschAlgorithmTests.cs

It was really fun learning more about quantum computing and implementing a basic quantum simulator. This was a brief introduction into the subject, which I tried to keep simple, and haven’t covered quantum operations involving imaginary numbers or gone too deep into the math.

If you find any problem in my quantum simulator code feel free to open an issue on github.

Six years (so far) developing and managing the same application has taught me a few lessons, one of them being the value of pursuing system design coherence. It’s a collective, rather than an individual, responsibility, requiring the entire development team commitment.

Coherence is defined as the quality of being logical, consistent and forming a unified whole. Which from my point of view directly relates to how system design should be handled:

• Logical: System design decisions should be justified, following a clear line of thought.
• Consistent: System design decisions should be compatible, in agreement, with its current state.
• Unified whole: System components should fit together, seamlessly working alongside each other.

Below are listed five major practical guidelines on how to manage system design coherence in software projects.

1 - Create and follow codebase conventions

This is one of the most basic yet beneficial measures you can adopt to improve code quality. It deals with how source code files are written and organized within your codebase.

We developers spend most of our time reading, not writing, code, hence it’s extremely important to define and enforce coding conventions up front in your product development life cycle targeting improved code readability.

I personally adopt a combination of organizational and clean coding conventions such as:

• Segment Files/Directories/Namespaces by domain
• Avoid multiple languages in one source file
• Class/Interface names should be nouns or noun phrases
• Function names should say what they do
• Avoid too many arguments in functions
• Avoid functions with too many lines
• Replace magic numbers with named constants
• Don’t comment intuitive code
• Discard dead code
• Where to declare instance variables
• Where to put braces
• Tabs vs spaces

And the list goes on…

As a result of following conventions source code will be uniform throughout the codebase, reducing the cognitive effort for searching and reading code files.

2 - Implement clear software architectures

The definition of software architecture is still a topic of debate, but there’s a general understanding that it deals with how software is developed both in terms of its physical and logical structure.

The codebase of a software project that doesn’t follow a clear architectural style, whatever it may be, deteriorates gradually as new, unstructured code is added to it, becoming harder to modify. Hence the importance of putting in the hours for the design and conservation of an adequate software architecture.

Unfortunately there isn’t a magic architecture that fits all use cases. You need to take into account several factors from your project for choosing the right path to follow.

To provide a couple of examples the monolithic architecture was standard a decade ago, before the microservices architecture gained traction. Like any other, it has several benefits and drawbacks, to name a few:

Pros:

• Shared Components: Monoliths share a single code base, infrastructure and business components can be reused across applications, reducing development time.
• Performance: The code execution flow is usually constrained to a single process, making it faster and simpler when compared to distributed code execution.

Cons:

• Tight Coupling: Code changes to shared components can potentially affect the whole system so it has to be coordinated meticulously.
• Scalability: You cannot scale components separately due to interdependencies, only the whole application.

figure 1. The Monolith

A software team working on a product that deals with complex data models and needs processing operations to be fast, performant and integrated may prefer to go for a monolithic application.

On the other hand the microservices architecture addresses many of the situations in which monoliths fail, being a great fit for distributed, large scale web applications:

Pros:

• Decoupled: The application can remain mostly unaffected by the failure of a single module. Also, code changes in one microservice wont impact others, providing more flexibility.
• Scalability: Different microservices can scale at different rates, independently.

Cons:

• DevOps: Deploying and maintaining microservices can be complex, requiring coordination among multiple services.
• Testing: You can effectively test a single microservice, but testing a distributed operation involving multiple microservices is more challenging.

figure 2. Microservices Architecture

Some architectural patterns are more concerned with the physical disposition of an application and how it’s deployed than with its logical structure. That’s why it’s also important to define a clear logical architecture to guide developers on how to structure code, so that everyone in your team understands how components talk to each other, how responsibility is segregated between modules, how to manage dependencies and what the code execution flow looks like.

3 - Fewer is better: Languages, Frameworks and Tools

With each additional language, framework and tool you introduce into your system comes an additional development and operational cost. This cost comes in different forms, which are illustrated in the following examples:

a) You are a member of development team highly experienced in Nginx + Python + PostgreSQL web applications. The team is fluent in this stack, the development pipeline is tidy and new features are delivered frequently. Then one day a developer decides to implement a new strategic feature using a different stack, say Apache + Java + MySQL, in which he is also highly experienced, but his colleagues aren’t. Now whenever this developer is busy and his colleagues have to implement a feature using the different stack they do so more carefully, since they aren’t quite familiar yet with all the programming language features, web server and database modes of operation, etc, as they are with the original stack. Thus, development time increases.

b) You have been assigned for managing a production environment of an application facing a considerable growth rate. Your goal is to deliver a SLA of 99.9% avaiability, which breaks down to only 8h of downtime per year. You gather the team to evaluate all technologies and plan the infrastructure required to support the growth rate: health checks, operational metrics, failure recovery, autoscaling, continuous integration, security updates. The plan is implemented and you start fine tuning the production environment, dealing with unforeseen events and issues. After much effort the production environment is stable and on its way to deliver that SLA, but you discover that a different tech stack was introduced and needs to be deployed. You’ll need to reevaluate the infrastructure. Also if the stack isn’t compatible with your current hosting environment it will potentially incur additional operational expenses.

These are just two illustrative situations, showing the impact of adopting additional technologies on development productivity, infrastructure complexity and operational expenses.

Of course, different technologies bring different possibilities. If we were to use only a limited set of technologies life as a developer would be much harder. For instance, there are scenarios where graph databases outperforms relational databases immensely. In these scenarios the choice is easy since the benefits outweighs the costs. The point is, you should always evaluate the long-term costs of a technological decision before making it to solve a short-term problem.

All right, but how does this relates to system design coherence?

Well, I believe that a system that is designed to avoid redundant technologies, that takes most out of its current stack, that has a stable production environment, whose team carefully evaluates structural changes and is able to sustain development productivity in the long run is a system that is clearly following the definition of “coherence”.

4 - Involve your team in system design decisions

As I’ve stated in the beginning of this article system design is a collective, shared responsibility. Individual, local actions have the potential to affect the system globally, so it’s essential that the development team is on the same page regarding the codebase conventions, employed architectures and the technology stack.

The most effective way to build this shared knowledge environment is to involve the team in system design decisions. The benefits are plenty:

• Individuals feel valued and part of the team
• Important decisions are challenged by the entire team before being made
• System design strengths and weaknesses are more clearly understood by everyone
• Creates a sense of collective accountability and trust

This doesn’t mean that every developer on the team should have equal decision power. Senior roles should certainly have more influence in decision making then junior roles. But it’s vital that everyone has the opportunity to give his opinion and participate. Less experienced developers will definitely grow from these proceedings.

At the same time the team must be aware of the productivity costs that arise when time is needlessly spent arguing about minor, trivial decisions. Optimize for speed, and focus on moving forward and delivering results rather than overcaring for details.

5 - The All-in rule

Efforts to refactor a system design should be conducted to completion (all-in), rather than being partially concluded. There’s a great risk of eroding your system design if developers feel free to apply different coding styles and architectural patterns locally whenever they see fit. Before too long you will end up with a disconnected, sometimes conflicting, system design.

By preserving your system design you’re also preserving the validity of your team’s shared knowledge about the system, which is extremely valuable. During development we make several assumptions on the behavior of the system based in this shared knowledge. Once it starts to lose validity unexpected issues start occurring, developers become justifiably less confident in the system design, implement features more carefully, losing productivity.

The challenge here is being open to improve your system design knowing that it can be exceptionally expensive to conduct a large system refactor up to completion. An approach I have used in a similar situation was to isolate refactored services behind an integration interface. The result was two independent system designs seamlessly working alongside each other, rather than having them mixed together:

figure 3. Integrated designs

These five guidelines have served me well over the past years, helping to keep productivity high, optimize resources and deliver up to the standards. It’s more a mindset than an actual process. Like all mindsets it should be constantly challenged and subject to improvement.