The consensus problem is a fundamental problem in multi-agent systems which requires a group of processes (or agents) to reliably and timely agree on a single data value. Although extensively discussed in the context of distributed computing it’s not exclusive to this field, also being present in our society in a variety of situations such as in democratic elections, the legislative process, jury trial proceedings, and so forth.
It’s solved through the employment of a consensus protocol governing how processes (agents) interact with one another. It may seem redundant but, to solve the consensus problem, first all processes agree to follow the same consensus protocol.
Some of these processes may fail or be unreliable in other ways (such as in a conflict of interest situation) so consensus protocols must be fault tolerant or resilient. The processes must somehow propose their candidate values, communicate with one another, and decide on a single consensus value.
In this post I review four major consensus protocols for solving the consensus problem based on my implementation of them, namely:
- Chandra–Toueg
- Ben-Or
- Basic Paxos
- Nakamoto Consensus
You can find supporting code for this analysis in this GitHub repository: ConsensusKit
Before getting started let’s recap the three key properties of consensus protocols and take a quick look at relevant terminology for this discussion.
Properties of a consensus protocol
Formally a consensus protocol must satisfy the following three properties:
Termination
- Eventually, every correct process decides some value.
Integrity
- If all the correct processes proposed the same value “v”, then any correct process must decide “v”.
Agreement
- Every correct process must agree on the same value.
These requirements are rather straight forward. “Termination” certifies the protocol is resilient to halting failures. “Agreement” deters any two correct processes from deciding on different values which would break consensus. Lastly “Integrity”, which is in fact flexible and may vary depending on application requirements, assures the protocol behaves in an expected and unbiased way.
Terminology
These terms are used throughout this post as well within the provided support source code.
Protocol
The official set of rules (“algorithm”) governing the behavior of processes for solving the consensus problem.
Process
An individual agent belonging to a larger group of agents collectively interested in reaching consensus. Processes can be “correct”, meaning they strictly adhere to the protocol and are not subject to failures, or “faulty”, meaning we cannot rely on them following the protocol at all times.
Instance
A well-defined round of interactions among processes under a consensus protocol. Depending on the underlying protocol one or multiple intances are required for reaching consensus.
Proposer
A process role. Processes under this role are entitled for proposing values. Any value agreed upon by all correct processes must have originated in a proposer.
Decider
A process role. Processes under this role are entitled for deciding on a value. Any value agreed upon by all correct processes must have been voted by at least one decider.
Archiver
An application or a subsystem that is responsible for persisting decided values and implementing a protocol’s specific data constraints.
Failure detector
An application or a subsystem that is responsible for the detection of node failures or crashes.
Majority
A protocol’s specific threshold requiring at least half of available votes, more when faulty processes are taken into account.
Quorum
A protocol’s specific threshold which ensures that a minimum number of participants (or votes) is met for taking an action.
With these definitions in place let’s move on to the implementation and review of each consensus protocol.
Protocol structure
My main goal has been to implement these four protocols in code to be able to run and evaluate them in a controlled environment. I was also interested in trying to spot structural similarities among them that could be extracted into a common base structure, promoting code reuse.
The result of my first coding iteration is displayed in the simplified class diagram below:
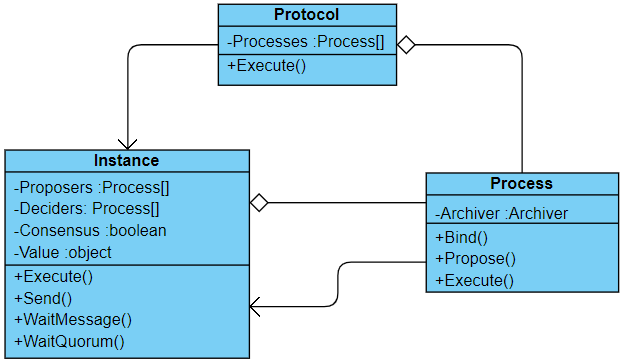
Three main classes are depicted in the diagram:
- The Procotol class has a collection of processes that will interact among each other according to the protocol rules for reaching consensus. Each execution of the protocol, through the
Executemethod, creates a new Instance (not to be confused with the conventional meaning of “instance” in object oriented programming). - The Instance class represents one round of interactions among processes potentially resulting in a consensus, as indicated by the
ConsensusandValueproperties. It’s responsible for managing the interaction between processes exercicing proposer and/or decider roles, providing methods for message delivery (Send) and retrieval (WaitMessageandWaitQuorum). - The Process class is responsible for implementing proposer and/or decider roles. Behavior is defined in the
Bindmethod just before the instance starts since, as well see, some protocols require processes to play different roles according the the current instance.
The Process.Propose virtual method is called at the start of an instance execution for all proposer processes in that instance to kick off communication and has the following default implementation:
protected virtual void Propose(Instance r)
{
var v = Proposer.GetProposal();
if (Archiver.CanCommit(v))
Broadcast(r, MessageType.Propose, v);
}
It first generates a proposal based on the underlying proposer logic (ex: random boolean proposer), then verifies against an archiver if the generated value passes custom application requirements and finally broadcasts it to all sibling processes.
Processes that bind to the Instance.WaitQuorum event will wait for the protocol specific amount of messages (for each message type) required for taking an action. The specific amounts are defined in each protocol implementation when deriving the Instance class.
All four consensus protocols were implemented using this base structure, as presented in the following sections. Rather than performing an extensive code analysis I will focus on presenting each theoretical algorithm and key points of my implementation.
1) Chandra–Toueg
The Chandra–Toueg consensus algorithm was first published by Tushar Deepak Chandra and Sam Toueg in 1996 and introduced the concept of failure detectors as means for solving the consensus problem. The algorithm assumes a number of faulty processes denoted by f that’s less than n/2 (i.e. less than simple majority).
In each instance one process acts as the decider (rotating coordinator) and all other processes act as proposers. The actions carried out in each instance are1:
- All processes send (r, preference, timestamp) to the coordinator.
- The coordinator waits to receive messages from at least half of the processes (including itself).
- It then chooses as its preference a value with the most recent timestamp among those sent.
- The coordinator sends (r, preference) to all processes.
- Each process waits (1) to receive (r, preference) from the coordinator, or (2) for its failure detector to identify the coordinator as crashed.
- In the first case, it sets its own preference to the coordinator’s preference and responds with ack(r).
- In the second case, it sends nack(r) to the coordinator.
- The coordinator waits to receive ack(r) or nack(r) from a majority of processes.
- If it receives ack(r) from a majority, it sends decide(preference) to all processes.
- Any process that receives decide(preference) for the first time relays decide(preference) to all processes, then decides preference and terminates.
Let’s take a look at the code. The following code snippet defines the proposer process behavior:
private void BindAsProposer(Instance r)
{
WaitQuorum(r, MessageType.Select, msgs =>
{
var m = msgs.Single();
SendTo(m.Source, r, MessageType.Ack, m.Value);
});
WaitQuorum(r, MessageType.Decide, msgs =>
{
var v = msgs.Single().Value;
Terminate(r, v);
});
}
On instance start proposers broadcast their values. Then they wait for a quorum to select a value from the pool of proposals. Since the protocol defines only a single decider per round this quorum is met when the decider process broadcasts his selection. Upon receiving this selection the proposer node will acknowledge it and wait for the decider’s decision, and then decide on the same value and terminate execution.
Now let’s see the code defining the complementary decider processes behavior:
private void BindAsCoordinator(Instance r)
{
WaitQuorum(r, MessageType.Propose, msgs =>
{
var v = PickMostRecentValue(
msgs.Where(m => Archiver.CanCommit(m.Value))
);
Broadcast(r, MessageType.Select, v);
});
WaitQuorum(r, MessageType.Ack, msgs =>
{
var v = PickMostRecentValue(msgs);
Broadcast(r, MessageType.Decide, v);
Terminate(r, v);
});
}
It first waits for a quorum of proposals, i.e, for a simple majority of proposers to submit their values. Then the decider picks the most recent message value, possibly validating the value with the archiver, and broadcasts the selected value back to all processes.
After broadcasting the selected value the decider waits for a quorum of proposers to acknowledge it, in which case it decides on that value and broadcasts its decision to all processes before terminating.
Notice that this simplified implementation doesn’t take failures into account, even though the Chandra–Toueg protocol is fault-resilient.
2) Ben-Or
Ben-Or is a decentralized consensus protocol, i.e., it doesn’t assign the decider role to any specific process. Curiously the algorithm correctness proof was only provided in a paper 15 years after its original publication2.
Because it lacks a decider for solving tie-break situations, Ben-Or is only capable of handling binary value consensus (“true” or “false”), rather than arbitrary value consensus. Even then, it employs randomization for converging to consensus.
The algorithm works in phases within instances and is resilient up to f crashing processes among a total of n processes given that n > 2f. Here are the actions performed by every process in an instance:
- Assign the process initial preference value x (0 or 1)
- Assing the phase number k to zero
- Loop:
- Increment the current phase number k
- Send (R, x, k) to all processes
- Wait for messages of the form (R, k, *) from n − f processes (“∗” can be 0 or 1)
- If received more than n/2 (R, k, v) with the same v Then
- Send (P, k, v) to all processes
- Else
- Send (P, k, ?) to all processes
- If received more than n/2 (R, k, v) with the same v Then
- Wait for messages of the form (P, k, ∗) from n − f processes (“∗” can be 0, 1 or ?)
- If received at least f + 1 (P, k, v) with the same v ≠ ? Then
- Decide(v) and terminate execution
- Else if at least one (P, k, v) with v ≠ ? Then
- Set x to v
- Else
- Set x to 0 or 1 randomly
- If received at least f + 1 (P, k, v) with the same v ≠ ? Then
It’s essentially a loop that ends when the process is able to decide on a value, otherwise it keeps going on, where each loop iteration is a new phase consisting of two asynchronous rounds.
In the algorithm, every message contains a tag (R or P), a phase number, and a value which is either 0 or 1 (for messages tagged P, it could also be “?”). Messages tagged “R” are called reports and those tagged with “P” are called proposals.
This protocol was the easiest to implement, but don’t fool yourself, in reality it’s behavior is not trivial to analyze, and that’s why it took so long for the correctness proof the come along. Below is my implementation of the Ben-Or process behavior:
public override void Bind(Instance r)
{
WaitQuorum(r, MessageType.Propose, msgs =>
{
var x = PickMostFrequentValue(
msgs.Where(m => Archiver.CanCommit(m.Value))
);
var v = x.Count > r.Proposers.Count / 2 ? x.Value : null;
Broadcast(r, MessageType.Select, v);
});
WaitQuorum(r, MessageType.Select, msgs =>
{
var x = PickMostFrequentValue(msgs.Where(m => m.Value != null));
if (x.Count >= f + 1)
{
Terminate(r, x.Value);
Proposer.Reset();
}
else
{
if (x.Count > 0)
Proposer.Set(x.Value);
else
Proposer.Reset();
}
});
}
I have replaced the “R” tag by the MessageType.Propose enum value and the “P” tag by the MessageType.Select for being more consistent with other protocol implementations within the repository. Aside from that it’s pretty much a copy of the algorithm described earlier, with the actual loop implemented in an event based manner, i.e., as a result of cyclic message passing between processes.
3) Basic Paxos
So I just learned that the Paxos family of protocols is as old as I am, being first submitted in 1989 (my year of birth) by Leslie Lamport. It’s name is derived after a fictional legislative consensus system used on the Paxos island in Greece, where Lamport wrote that the parliament had to function “even though legislators continually wandered in and out of the parliamentary Chamber”.
Paxos was by far the toughest one to reason about and implement in code. In it processes are classified as proposers, accepters, and learners (a single process may have all three roles). The idea is that a proposer attempts to ratify a proposed decision value (from an arbitrary input set) by collecting acceptances from a majority of the accepters, and this ratification is observed by the learners. Agreement is enforced by guaranteeing that only one proposal can get the votes of a majority of accepters, and validity follows from only allowing input values to be proposed3.
The basic Paxos algorithm is briefly presented below:
- The proposer sends a message prepare(n) to all accepters. (Sending to only a majority of the accepters is enough, assuming they will all respond.)
- Each accepter compares n to the highest-numbered proposal for which it has responded to a prepare message. If n is greater, it responds with ack(n, v, nv) where v is the highest-numbered proposal it has accepted and nv is the number of that proposal (or ⊥, 0 if there is no such proposal).
- The proposer waits (possibly forever) to receive ack from a majority of accepters. If any ack contained a value, it sets v to the most recent (in proposal number ordering) value that it received. It then sends accept(n, v) to all accepters (or just a majority).
- Upon receiving accept(n, v), an accepter accepts v unless it has already received prepare(n’) for some n’ > n. If a majority of acceptors accept the value of a given proposal, that value becomes the decision value of the protocol.
Note that acceptance is a purely local phenomenon, so I’ll be including an additional message passing step in my implementation intended to detect which if any proposals have been accepted by a majority of accepters before processes can reliably decide on a value.
Now let’s look at the code implementation starting with the the proposer role behavior:
protected override void Propose(Instance r)
{
proposalNumber = minNumber + 1;
Broadcast(r, MessageType.Propose, proposalNumber);
}
private void BindAsProposer(Instance r)
{
WaitQuorum(r, MessageType.Ack, msgs =>
{
var v = PickHighestNumberedValue(msgs)?.Value ?? Proposer.GetProposal();
if (Archiver.CanCommit(v))
{
var x = new NumberedValue(v, proposalNumber);
Broadcast(r, MessageType.Select, x);
}
});
WaitMessage(r, MessageType.Nack, msg =>
{
if (msg.Value != null)
{
var n = (long)msg.Value;
if (n > minNumber)
{
minNumber = Math.Max(n, minNumber);
if (RandomExtensions.Tryout(0.5))
Propose(r);
}
}
});
WaitQuorum(r, MessageType.Accept, msgs =>
{
var m = msgs.Select(m => m.Value).Distinct();
if (m.Count() == 1)
{
var x = m.Single() as NumberedValue;
Terminate(r, x);
Broadcast(r, MessageType.Decide, x);
}
});
}
Obs: Usage of Math.Max in this snippet may seem redundant, but it was actually employed to solve a race condition without resorting to a mutex.
You can see that in this case the Process.Propose method was overridden to implement the Paxos protocol proposal numbering logic, and that I’ve used the MessageType.Propose enum member to represent the “prepare” message.
After broadcasting its proposal number the process will wait for either MessageType.Ack or MessageType.Nack responses. In case it receives a negative response this means its proposal number is outdated, so the process will update it and submit a new proposal (after a random interval added for debugging purposes). However, in case it receives enough positive responses to form a quorum the process will broadcast a MessageType.Select message representing the proposer’s accept vote (the algorithm’s third step) for the highest numbered value it’s seen so far, or it’s own preferred value if it hasn’t seen one yet.
Lastly, the proposer will be waiting for a quorum of consistent MessageType.Accept messages from accepters to learn which value has been accepted by a majority of them, in which case it decides on that value and terminates.
On the other side of the picture we have accepters, whose behavior code is presented below:
private void BindAsAccepter(Instance r)
{
WaitMessage(r, MessageType.Propose, msg =>
{
var n = (long)msg.Value;
if (n > minNumber)
{
minNumber = n;
SendTo(msg.Source, r, MessageType.Ack, accepted);
}
else
{
SendTo(msg.Source, r, MessageType.Nack, minNumber);
}
});
WaitMessage(r, MessageType.Select, msg =>
{
var x = msg.Value as NumberedValue;
if (x.Number >= minNumber && Archiver.CanCommit(x.Value))
{
accepted = x;
SendTo(msg.Source, r, MessageType.Accept, x);
}
});
WaitMessage(r, MessageType.Decide, msg =>
{
var x = msg.Value as NumberedValue;
Terminate(r, x);
});
}
Upon receiving MessageType.Propose messages the accepter will “ack” as long as the proposal number is greater than the highest proposal number it’s seen so far (minNumber), updating that number, or “nack” considering it’s smaller than or equal.
Then it waits for MessageType.Select messages and accepts it as long as the proposal number is greater than or equal minNumber, in which case it updates its lastly accepted value and sends a MessageType.Accept message back to the proposer.
In closing, the accepter simply waits for a MessageType.Decide to decide on its value and terminate execution.
4) Nakamoto Consensus
In the Bitcoin white paper, Nakamoto proposed a very simple Byzantine fault tolerant consensus algorithm that is also known as Nakamoto consensus. It’s fundamentally a randomized consensus protocol that employs the concept of “Proof of Work” for defining which process is entitled to legitimately decide on a value.
This proof of work operation is asymmetric, hard to conclude but easy to verify. This is necessary to achieve a functional randomized behavior that is the basis of the protocol, otherwise it would be very difficult for processes to agree on the validity of proposed values.
Nakamoto consensus has its own terminology. Instead of “values” processes seek to reach consensus on data “blocks”. As the protocol execution advances the set of decided data blocks form a “chain” with each new block reinforcing the previous chain block. The act of delivering a proof of work on a block, in order for a process to propose that block to the network, is called “mining”.
The algorithm can be briefly described in two sentences as follows4:
- At each round r, an honest process attempts to mine new blocks on top of the longest chain it observes by the end of round
r − 1(where ties can be broken arbitrarily). This is often referred to as the longest chain rule. - At each round r, an honest process confirms a block if the longest chain it adopts contains the block as well as at least k other blocks of larger heights. This is sometimes referred to as the k-deep confirmation rule.
The purpose of the k-deep confirmation rule is to reduce the chances of a process deciding on an uncertain/volatile data block to a negligible probability.
Even though the Nakamoto consensus protocol has a simple form, it requires a reasonable amount of code for implementing the block mining and block chains management logic. Here’s my implementation top level code:
protected override void Propose(Instance r)
{
ThreadManager.Start(() =>
{
var b = MineBlock(r);
if (b != null)
{
ProcessBlock(r, b);
Broadcast(r, MessageType.Propose, b);
}
});
}
public override void Bind(Instance r)
{
WaitMessage(r, MessageType.Propose, msg =>
{
var b = msg.Value as Block;
ProcessBlock(r, b);
});
}
private void ProcessBlock(Instance r, Block b)
{
if (b.VerifyPoW())
{
var newChain = AddNewChain(b);
if (IsKDeep(newChain) && !IsTerminated(r))
{
Terminate(r, GetBlockAt(newChain, k).Value);
CommitChain(newChain);
}
}
}
Since mining a block is a time consuming operation it’s performed within a thread and, unlike other protocols described earlier, the proposal phase becomes asynchronous. Upon receiving a proposal the process will evaluate whether the proposed block is valid, i.e., if it’s possible to verify its proof of work. Then, the block is added to a compatible chain found in the set of unconfirmed chains. Finally, if the resulting unconfirmed chain segment becomes k-deep the process will decide on its oldest unconfirmed block.
Conclusion
Taking as base components and terminology described in the literature for coding these four major consensus protocols allowed for the abstraction of structural and message routing logic away from each specific protocol implementation in a consistent manner. The end result highlights each protocol logic and behavior making the code more readable and succinct.
Alternatives to improve the current achitecture and proceed with this study include i) refactoring the Instance class to extract event biding and message passing responsabilities into new components and ii) implement supporting components for evaluating protocol performance in the presence of process failures/crashes.
This exercise has been extremely helpful to me to better understand the consensus problem and have a glimpse into different approaches for solving it. I hope it may serve as a starting point for others interested in learning the basics of consensus protocols in a more practical way.
Notes
- Revised on Oct 29, 2020. For reference you can find the original article here.
Sources
[1] Wikipedia. Chandra–Toueg consensus algorithm.
[2] Marcos Kawazoe Aguilera, Sam Toueg. Correctness Proof of Ben-Or’s Randomized Consensus Algorithm. 1998.
[3] James Aspnes. Paxos - Class notes. 2003 to 2012.
[4] Jianyu Niu, Chen Feng, Hoang Dau, Yu-Chih Huang, and Jingge Zhu. Analysis of Nakamoto Consensus, Revisited. 2019.